如何將交互式的零知識證明（zk proof）協議改造為非交互式_COM

密碼學當中的零知識證明技術在 web3 世界有著廣泛的應用，包括進行隱私計算、zkRollup 等等。其中 Layer2 項目 FOX 所使用的 FOAKS 就是一個零知識證明算法。在上述的一系列應用當中，對于零知識證明算法而言，有兩方面屬性極為重要，那就是算法的效率以及交互性。

算法效率的重要性不言而喻，高效的算法可以明顯的降低系統運行時間，從而降低客戶端延遲，顯著的提高用戶體驗和效率，這也是 FOAKS 致力于實現線性證明時間的一個重要原因。

另一方面，從密碼學的角度來講，零知識證明系統的設計往往依賴證明者和驗證者的多輪交互。例如在許多介紹零知識證明的科普文章當中都會使用的“零知識洞穴”的故事當中，證明的實現就依賴于阿里巴巴（證明者）和記者（驗證者）多輪的信息傳遞交互才能實現。但是事實上，在許多應用場景當中，依賴交互會使得系統不再可用，或者極高的增加延遲。就像在 zkRollup 系統當中，我們期望證明者（也就是 FOX 當中的 folder）能夠在本地，不依賴于和驗證者交互的情況下就計算出正確的證明值。

從這個角度說，如何將交互式的零知識證明協議改造為非交互式，就是一個很有意義的問題。在這篇文章當中，我們將介紹 FOX 使用經典的 Fiat-Shamir 啟發式（heuristic）來生成 Brakedown 中的挑戰從而實現非交互式協議的過程。

零知識證明算法隨著應用的鋪開而變得異常火爆，近些年也誕生了包括 FOAKS、Orion、zk-stark 等在內的各種算法。這些算法，以及密碼學界早期的 sigma 協議等的核心證明邏輯都是證明者（Prover）先將某個值發送給驗證者（Verifier），驗證者通過本地隨機數產生一個挑戰（Challenge），將這個隨機產生的挑戰值發給證明者，證明者需要真的有知識才能以大概率做出通過驗證者的響應。例如在零知識洞穴當中，記者拋一個硬幣，告訴阿里巴巴從左側出來還是從右側出來，這里的“左和右”就是對阿里巴巴的挑戰，他如果真的知道咒語，就一定可以從要求的方向走出來，否則就有一半的概率失敗。

Sweat授權社區決定如何處理自年初以來積累的1億枚SWEAT代幣:4月18日消息，Move-to-Earn 項目 Sweat 授權社區決定如何處理自今年年初以來積累的 1 億枚 SWEAT 代幣，投票選項包括 0% 分發和 100% 銷毀，25% 分發和 75% 銷毀，50% 分發和 50% 銷毀，75% 分發和 25% 銷毀，100% 分發和 0% 銷毀。[2023/4/18 14:11:30]

這里我們注意到，Challenge 的生成是一個很關鍵的步驟，它有兩個要求，隨機和不可被證明者預測。第一點，隨機性保證了它的概率屬性。第二點，如果證明者可以預測挑戰值那就意味著協議的安全性被破壞了，證明者沒有知識也可以通過驗證，可以繼續類比，阿里巴巴如果能預測記者要求他從哪邊出來，他即使沒有咒語也可以提前進入那一邊，結果表現出來一樣可以通過協議。

所以我們需要一種辦法，能夠讓證明者自己本地生成這樣一個不可預測的隨機數，同時還能夠被驗證者驗證，這樣就可以實現非交互式的協議。

哈希函數的名字對我們來說或許并不陌生，無論是在比特幣的共識協議 POW 當中擔任挖礦的數學難題，還是壓縮數據量，構造消息驗證碼等等，都有哈希函數的身影。而在上述不同的協議當中，其實是運用了哈希函數的各種不同性質。

具體來講，安全的哈希函數的性質包括以下幾點：

壓縮性：確定的哈希函數可以將任意長度的消息壓縮成為固定長度。

觀點：目前行業內是一個沉淀期，builders應該更多去focus在如何解決問題:近日，BeWater DevCon 2022 全球開發者大會在硅谷灣區成功舉辦，來自Polychain Capital, Uphonest Capital, DFG Capital, Foresight Ventures的嘉賓進行了圓桌討論，圍繞“VC如何在熊市中投資和支持Builders”。Polychain Capital的Jacob Philips表示，目前行業內是一個沉淀期，builders 應該更多去focus在如何解決問題。Uphonest Capital的KJ表示，VC應該作為共同創業的伙伴，而不僅僅是投資就不管事兒了。DFG Capital的Joanna表示，這個熊市的基本面已經和18年19年的熊市大不一樣，基礎設施得到大量發展，讓大家多多探索

Foresight Ventures的Suning表示，builder可以在熊市多做一些新嘗試，比如在開發語言方面，嘗試Move或Cairo，探索全新生態的可能性。同時作為Foresight Ventures也會更多關注真正顛覆性的創新，以及圍繞DAO或者NFT等的crypto-native的文化發展。[2022/6/24 1:29:46]

有效性：給定輸入 x，計算輸出 h（x）是容易的。

抗碰撞性：給定一個輸入 x1，希望找到另一個輸入 x2，x1x2，h（x1）= h（x2），是困難的。

北冥社區創始人北冥：數字資產價格走勢無法提前預知，核心在于如何應對:6月19日19:00，MXC抹茶特邀分析師，北冥社區創始人北冥做客MXC抹茶社區進行分享。北冥表示：“交易是對認知的變現，通過數字資產交易獲取收益，離不開技術分析。均線纏論系統，有助于遠離盲目多空。“中樞”一詞源自《纏論》第108課，《纏論》作者禪師通過歸納演繹等數學方法，對任何走勢進行統一的定義和分類，并給出一個較為合理的解決方案，《纏論》最厲害的地方就是“完全分類“，大部分走勢都是無法提前被預知的，核心就在于應對。纏者，價格重疊區間也，買賣雙方陣地戰之區域也；禪者，破解之道也。以陣地戰為中心，比較前后兩段之力度大小。大者，留之，小者，去之。”[2020/6/19]

注意，如果哈希函數滿足抗碰撞性，那么必然滿足單向性，也就是說給定一個輸出 y，要找出 x 滿足 h（x）= y 是困難的。在密碼學當中，還不能構造出理論上絕對滿足單向性的函數，但是哈希函數在實際應用當中可以基本視作單向函數。

這樣一來，可以發現上述的幾種應用分別對應于哈希函數的幾點不同的性質，同時我們說，哈希函數還有一個很重要的作用是提供隨機性，雖然密碼學理論當中要求的完美的隨機數生成器目前也無法構造，但是哈希函數在實際當中同樣可以充當這個角色，這就為我們后文介紹的 Fiat-Shamir 啟發式（Heuristic）的技巧提供了基礎。

事實上，Fiat-Shamir 啟發式（Heuristic）就是利用哈希函數來對前面生成的腳本進行哈希運算，從而得到一個值，用這個值來充當挑戰值。

聲音 | 光大證券彭文生：Libra的發展關鍵要看監管機構如何在支持創新和監管之間的平衡:近日，光大集團研究院副院長、光大證券全球首席經濟學家彭文生表示，和比特幣等代幣相比，Libra尚未問世引來如此高的關注度，一是數字經濟下科技巨頭平臺公司和貨幣的網絡規模優勢有協同效應；二是Libra作為一攬子貨幣的衍生品，屬于數字貨幣中的穩定幣。而比特幣等代幣僅僅是數字資產，其未來價值取決于使用者對其的“信仰”，故其價格波動幅度會比較大。他還指出，未來Libra要成為貨幣，在起步階段，支付手段可能是突破口；但發展到一定規模后，儲值工具的作用更重要，是推動Libra能成為一種真正貨幣的主要力量。Libra現在是0，按常理起步會較慢，但不能低估其社區網絡帶來的規模效應。不過Libra的發展關鍵還要看監管機構如何在支持創新和監管之間的平衡。[2019/7/30]

因為將哈希函數 H 視作一個隨機函數，挑戰是均勻隨機的被選擇，獨立于證明者的公開信息和承諾的。安全分析認為 Alice 不能預測 H 的輸出，只能將其當作一個 oracle。在這種情況下，Alice 在不遵循協議的情況下做出正確響應的概率 ( 特別是當她不知道必要的秘密時 ) 與 H 的值域的大小成反比。

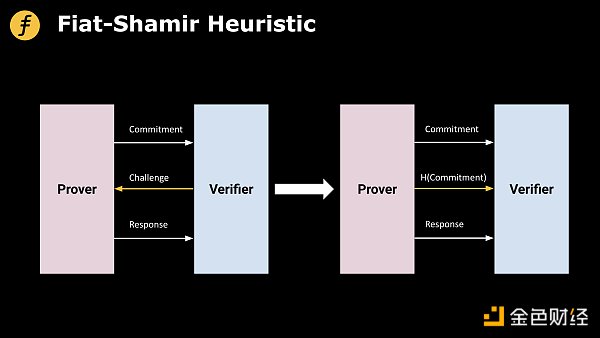
圖 1: 利用 Fiat-Shamir Heuristic 實現非交互式證明

中紀委機關報談區塊鏈發展：如何讓監管理解并適度監管是挑戰:今日東方財富網發文稱，在今年的全國兩會上，“區塊鏈”成為一些代表委員熱議的話題，近日中紀委機關報談到區塊鏈發展時，認為：如何讓監管理解并適度監管是挑戰。[2018/3/6]

在本節，我們具體展示 Fiat-Shamir 啟發式在 FOAKS 協議當中的應用，主要是用來產生 Brakedown 部分的挑戰，從而實現非交互式的 FOAKS。

首先我們看到，在 Brakedown 生成證明的步驟當中，需要挑戰的步驟是“近似性檢驗”以及 Merkle Tree 的證明部分（讀者可以參考之前的文章《一文了解 FOAKS 當中的多項式承諾協議 Brakedown》）。對于第一點原本的過程是證明者在這里需要驗證者產生的一個隨機向量，計算過程如下圖所示：

圖 2: 非交互證明 FOAKS 中的 Brakedown Checks

現在我們使用哈希函數，讓證明者自己產生這個隨機向量。

令γ0=H(C1,R, r0,r1)，對應的，在驗證者的驗證計算當中，也需要增加這個計算出γ0的步驟。根據這樣的構造，可以發現，在生成承諾之前，證明者并不能提前預測挑戰值，于是不能提前根據挑戰值來對應的“作弊”，也就是對應的生成假的承諾值，同時，根據哈希函數輸出的隨機性，這個挑戰值也滿足隨機性。

對于第二點，令 ? =H(C1,R, r0,r1,c1,y1,cγ0,yγ0)。

我們使用偽代碼給出改造后非交互式的 Brakedown 多項式承諾當中的證明和驗證函數，這也是 FOAKS 系統當中使用的函數。

function PC. Commit(?)：

Parse was a k × k matrix. The prover locally computes the tensor code encoding C1，C2 ，C1 is a k × n matrix，C2 is a n × n matrix.

for i ∈ [n] do

Compute the Merkle tree root Roott=Merkle.Commit(C2[:,i])

Compute a Merkle tree root R=Merkle.Commit([Root0,......Rootn-1]),and output R as the commitment.

function PC. Prover(?, X, R)

The prover generates a random vector γ0 ∈ Fk by computing: γ0 =H(C1,R, r0,r1)

Proximity:

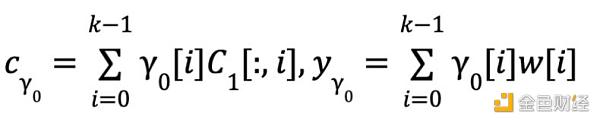
Consistency:

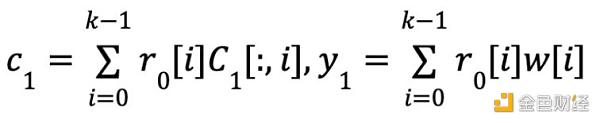
Prover sends c1,y1,cγ0,yγ0 to the verifier.

Prover computes a vector ? as challenge, in which ? = H(C1,R, r0,r1,c1,y1,cγ0,yγ0)

for idx ∈ ? do

Prover sends C1 [:,idx] and the Merkle tree proof of Rootidx for C2 [:,idx] under R to verifier

function PC. VERIFY_EVAL(ΠX,X,y= ? (X),R)

Proximity: ?idx ∈ ?, Cγ0 [idx] == and Ec(yγ0) == Cγ0

Consistency: ?idx ∈ ?, C1 [idx] == and Ec(y1) == C1

y==1, y1>

?idx ∈ ?, Ec ( C1[:,idx]) is consistent with ROOTidx, and ROOTidx’s Merkle tree proof is valid.

Output accept if all conditions above holds. Otherwise output reject.

許多的零知識證明算法在設計之初都依賴證明者和驗證者雙方的交互，但是這種交互式證明協議不適合用在追求高效，網絡通訊開銷大的應用場景下，比如鏈上數據隱私保護和 zkRollup 等等。通過 Fiat-Shamir 啟發式（Heuristic），可以在不破壞協議安全性的條件下讓證明者本地生成隨機數“挑戰”，并且可以被證明者驗證。根據這種方法，FOAKS 同樣實現了非交互式的證明，并應用在系統當中。

1.Fiat, Amos; Shamir, Adi (1987). "How To Prove Yourself: Practical Solutions to Identification and Signature Problems". Advances in Cryptology — CRYPTO' 86. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 263: 186–194. doi:10.1007/3-540-47721-7_12. ISBN 978-3-540-18047-0.

2.https://www.cnblogs.com/zhuowangy2k/p/12246575.html

撰文：康水躍，Fox Tech CEO；孟鉉濟，Fox Tech 首席科學家

來源：DeFi之道

DeFi之道

個人專欄

閱讀更多

金色財經 善歐巴

金色早8點

白話區塊鏈

Odaily星球日報

MarsBit

歐科云鏈

深潮TechFlow

Arcane Labs

BTCStudy

Tags：PROIDXVERCOMBribe ProtocolIDX價格Xenoverse CryptoComBit

屎幣