【密碼專欄】超強進階：PLONK VS Groth16（上）_PLO

前言

前文《天冷了，干了這碗“零知識證明”雞湯》對「零知識證明學習」作了一個形象化的比喻：燉雞湯。那么本系列的主要內容可以簡單概括為《論高壓鍋燉雞湯的一百種方法》之方法二。在學會了“清燉雞湯”之后，不如來一口“阿膠雞湯”補補腦細胞吧！

正如雞湯不同風味之間各具千秋，不同的zk-SNARK方案也各有所長。zk-SNARK方案可以被分為與zk-SNARK，PLONK與Groth16分別是其中的典型代表。通過本系列，我們將對PLONK算法內容作簡要介紹，并指出PLONK和Groth16算法思路上的異同。

PLONK算法在中提出，由來自于ProtocolLabs的研究員Gabizon和以太坊隱私交易協議AztecProtocol的兩名研究人員合作完成。PLONK的提出晚于Groth16，在證明和驗證的性能上與Groth16也存在一定差距，但是基于通用可更新的可信設置這一特點，使PLONK算法在零知識證明領域占據了一席之地。

可信設置

可信設置可以說是PLONK和Groth16兩者間最顯著的差異。正是為了避免一次性的可信設置，PLONK設計了后續的約束系統和問題壓縮方式。那么什么是零知識證明中的可信設置呢？可信設置實際上是在創建一個用于證明驗證的秘密，任何知道這個秘密的人都可以偽造證明通過驗證。如果將零知識證明看作是一扇擋在證明者a和驗證者b之間上鎖的門，那么合法構建的證明就是可以打開門的口令，a提供口令即可進入房間。但是如果a得知了門的秘密也就是房間窗戶的位置，那么a可以直接無視鎖的存在翻窗進入房間。

基于閃電網絡的小額支付服務公司Bitcache進入清算程序:金色財經報道，由Megaupload創始人Kim Dotcom創建的基于閃電網絡的小額支付服務公司Bitcache在推出失敗后已進入清算程序。該公司于2016年首次宣布，旨在整合到Dotcom的數字市場 K.im。Bitcache前董事Phil Creagh曾在5月份申請將公司置于清算狀態。Creagh聲稱，這非常簡單，有欠費用但未支付。迄今為止，該公司尚未采取任何措施來避免被清算。[2023/7/13 10:53:00]

▲無窗的房間

顯然，最安全的做法是找一個「沒有窗的房間」，這也是一部分零知識證明方案的思路——無需可信設置，例如可擴展透明知識論證zk-STARKs和防彈證明Bulletproofs。雖然它們的安全性得到提高，但是目前這類方法的證明驗證性能是遠低于zk-SNARKs的，近線性的驗證和規模較大的證明使其不適用于很多場景。

▲窗戶位置指定策略

PLONK和Groth16的做法都是保留窗戶，但是盡力保護窗戶的位置不被別人知道。

Groth16的做法是：根據不同的問題，每次都指定窗戶在房間中的擺放位置，也就是它需要一次性的可信設置。而PLONK面對不同的問題時：窗戶的位置是固定不變的，即窗戶的位置只需要被指定一次。也就是說PLONK的可信設置是通用的。那么這些窗戶指定的位置由誰來確定呢？當然，可信第三方是一個備選項。但這意味著說這間房間是否會被惡意證明者攻破，其安全性寄希望于這位第三方。除此之外還有一項熱門技術也可為其提供思路——多方安全計算。沿用之前的例子，可以不太嚴謹地將MPC概括為：多個人共同指定窗戶的位置，除非這些參與者全部聯合起來對答案，這個位置將無法由任何人得知。

支付解決方案Poko完成450萬美元種子輪融資:6月15日消息，支付解決方案Poko宣布完成450萬美元的種子輪融資，Y Combinator、Goodwater Capital和Global Founders Capital等參投，Poko計劃為錢包、錢包即服務提供商提供無摩擦支付。[2023/6/15 21:39:07]

顯然，使用MPC時，參與者的數量越多，秘密的安全性越高，這類可信設置也比可信第三方更為用戶所接受。遺憾的是，雖然目前提出了基于Groth16的可信設置，但是由于Groth16的秘密計算與特定的問題相關聯，每次遇到新的問題時，必須重新開啟一輪MPC可信設置。可想而知，需要多方參與的計算協議將是極為繁瑣的，這樣將大大影響Groth16的性能。相比之下，具備通用性的PLONK與MPC的適配度極高。

而之前提到的PLONK可信設置的可更新性則是指：通用的PLONK秘密可以通過再開啟一輪MPC作更新。新生成的秘密安全性建立在兩次MPC的安全性上，只要兩次中有一個參與者是誠實的，這個秘密就是可信的。約束系統

Groth16及PLONK均將程序先轉化為一個由加法門和乘法門組成的算術電路，再通過將電路構建為多項式的形式來進行后續的計算。本節我們將使用Vitalik文章中的一個簡單例子進行說明：

工信部官員：加強頂層設計，加快元宇宙產業創新發展:金色財經報道，在27日舉行的XRMID2023虛擬現實及元宇宙產業創新發展峰會上，中國工業和信息化部科技司副司長任愛光表示，將加強頂層設計，加快元宇宙產業創新發展，通過揭榜掛帥、建設先導區等方式，積極推動人工智能、區塊鏈、虛擬現實等元宇宙支撐技術的創新發展，夯實產業發展的根基。[2023/5/1 14:36:35]

對于程序qeval,prover需要證明自己知道qeval(x)=35的解，即x=3。

defqeval(x):

y=x**3

returnx+y+5，其轉化為算術電路可表示如下：

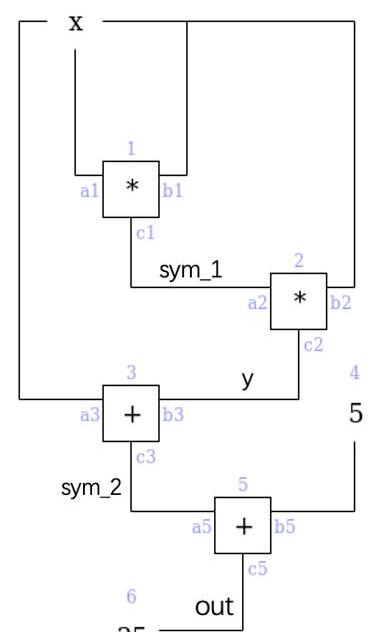
PLONK中，上圖電路的描述由兩部分組成：門約束與線約束。門約束固定電路中每個門的動作。此外，在電路中我們規定相連線的值應保持一致，對此線約束規定這些線的關系。接下來我們分別討論兩類約束的多項式表示。門約束

在PLONK中，對于第i個門，可被描述為如下形式：

Delphi研究員：特朗普NFT系列團隊被質疑私自鑄造了1000枚NFT:12月19日消息，Delphi Research研究員TengYan在社交媒體表示，特朗普NFT系列團隊在其金庫地址鑄造了1000枚NFT，為自己保留了許多稀有的、包括親筆簽名的1-of-1NFT。Teng Yan表示，“我懷疑特朗普甚至不知道這件事，懷疑他委托做NFT的團隊找到了一種從游戲稀有分布中獲利的方法”。

據OpenSea數據顯示，截至發稿時，Trump Digital Trading Cards地板價為0.2848ETH，24小時跌幅達57%。[2022/12/19 21:53:07]

（QLi)ai+(QRi)bi+(QOi)ci+(QMi)aibi+Qci=0

其中Q均為常數，a,b,c則是信號的下標。具體地，在PLONK中門約束可以被分為三類：算術約束、布爾約束、公共輸入約束。

最為常見，用于表示電路中的所有加法門和乘法門，此時a,b,c分別表示門的左右輸入和輸出信號下標，Q_C一般為0。根據門的類型剩余的符號有不同的取值：

加法門：QLi=1，QRi=1，QOi=-1，QMi=0??ai+bi-ci=0乘法門：QLi=0，QRi=0，QOi=-1，QMi=1-ci+?aibi=0

美執法部門已追回3000萬美元的Ronin被盜資金:9月8日消息，美國執法部門已追回3000萬美元的Ronin Network被盜資金。此前參與此次被盜資金追蹤的安全機構Chainalysis表示，被追回的資金來自于被幣安凍結的580萬美元以及在其他交易所被凍結的資金。Chainalysis并未透露其他交易所的名字，但表示聯邦調查局參與了本次調查。（華爾街日報）[2022/9/9 13:18:05]

顧名思義，用于約束布爾類型的信號，其值只能取0或1。例如現在需要約束下標為j的信號∈{0,1}，那么門約束式子中各變量的取值為：

ai=bi=j，QLi=-1，QMi=1，QOi=QRi=Qci=0

-j+j*j=0

另外，針對問題中出現的證明方和驗證方都知道取值的輸入，需要在約束系統中有所體現。例如要求約束下標j的信號取值為v，對應的取值為：

ai=j，QLi=1，QMi=QOi=QOi=0，Qci=-v

j-v=0

利用該式，我們可以很容易地表示上圖中的所有門約束：

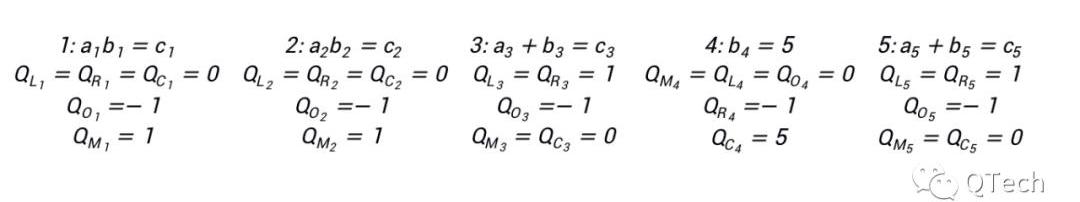
與Groth16類似，可以將所有的多項式組整合在一個多項式中：

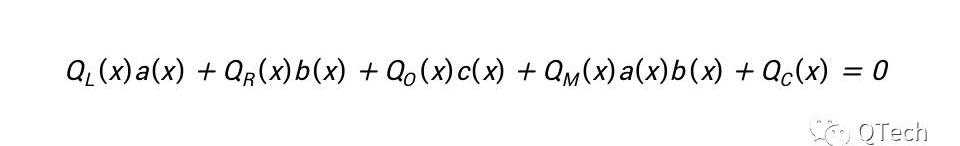
線約束

線約束可以分為兩種情況：

同一多項式內部，例如：a1=a3

不同多項式之間，例如：a1=b1

當只需要考慮情況1時，可以通過構造p(x)=P(x)來實現約束：

X(X)=X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

其中β,γ為隨機數，X->Y表示了待約束的多項式，P(x)使用了x的置換σ(x)。對于下面例子：

X(1)→Y(1)

X→Y：X(2)?→?Y(2)?and，Y(1)=Y(3)

X(3)→?Y(3)

σ(1)=3

σ(X)：σ(2)=2

σ(3)=1

當且僅當Y(1)=Y(3)成立時，p(x)=P(x)。

現在，讓我們增加問題的復雜度：需要約束的多項式個數為k時。自然地，設門的總數為n，我們可以對第j個多項式構造對應的p_j(x)=P_j(x)，即

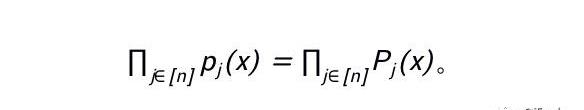
進一步地，情況2的出現要求對以下情況中的x作區分：

pj(x)and?pi(x)????

那么可以增加對x的映射，對于第j個多項式：

X(X)=(j-1)*n+X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

以上就是線約束的全部內容，其實質是為了保證電路中同一條或相連線上的值相等。

與Groth16類似，將上述的約束聯立將得到一個完整的PLONK約束系統。通過將抽象的代碼和電路轉化為約束系統R1CS，我們可以將一個零知識證明問題固定下來。讓我們帶著問題進入下篇：PLONK中如何將R1CS轉為多項式描述？它與Groth16做法區別在何處？敬請期待！

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.(2019).PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.

SeanBoweand?ArielGabizonandIanMiers.(2017).ScalableMulti-partyComputationforzk-SNARKParametersintheRandomBeaconModel.

https://vitalik.ca/general/2019/09/22/plonk.html

Tags：PLOLONROTGROPLOCK價格Musk MelonPhantom ProtocolPOOGROW

以太坊