數字簽名：基于橢圓曲線的簽名方案_數字金融

在數字時代中，數字化文檔的認證性、完整性和不可否認性，是實現信息化安全的基本要求。數字簽名則是滿足上述要求的主要方式之一，亦是現代密碼學的研究內容之一。

數字簽名有哪些形式？基于密碼學的數字簽名優勢幾何？有哪些常用的數字簽名實現方案？使用過程中又潛藏何等風險？我們將先從理解概念為始，再為大家逐步深入介紹。

區塊鏈百科No.34：基于橢圓曲線簽名方案

隨著計算機信息處理能力的不斷提高，對密鑰長度的要求也越來越高，這個問題對于存儲能力受限的系統來說顯得尤為突出。

橢圓曲線密碼體制（ECC）的提出改變了這種狀況，它可以用更短的密鑰提供與其他體制相當的或者更高級的安全，并已成為迄今被實踐證明安全、有效、應用較廣的3種公鑰密碼體制之一。本文將繼續為大家介紹基于橢圓曲線的數字簽名方案。

Rivvoo潤沃《元藏家》元宇宙頭像創世數字藏品將于3月22日上線:據官方消息，Rivvoo潤沃《元藏家》元宇宙頭像創世數字藏品將于3月22日上線。《元藏家》是由Rivvoo潤沃聯合Metapapa推出的元宇宙頭像創世項目。此次《元藏家》采用數字水印技術，每個元藏家頭像都是獨一無二且都含有數字版權。區塊鏈+數字水印技術的結合，實現了鏈上存證+數字物理驗證的雙重保障，為數字藏品的發展和傳播奠定了穩固基礎。

據悉，Rivvoo潤沃是北京798藝術園區的一家專業的數字藏品平臺，其愿景是通過元宇宙和數字生態場景助力用戶獲得數字財富和事業成功。[2022/3/20 14:07:46]

橢圓曲線在代數學和幾何學上，已被廣范研究了150年之久，有堅實的理論基礎。

所謂橢圓曲線是指維爾斯特斯拉（Weierstrass）方程：

加拿大央行總裁：全球貨幣和金融體系必須向前發展以應對數字貨幣等未來挑戰:金色財經報道，加拿大央行總裁麥克勒姆周四表示，全球貨幣和金融體系必須向前發展，以應對退出非常規貨幣政策、氣候變化和數字貨幣等未來挑戰。麥克勒姆強調了向凈零排放的過渡以及可能的貨幣體系數字化，并提出需要一個處理，甚至促進未來過渡的國際貨幣和金融體系。（路透社）[2021/10/8 20:13:53]

所確定的平面曲線，其中a、b、c、d、e屬于域F，其可以是有理數域Q、復數域C，還可以是有限域GF（p）。

橢圓曲線是其上所有點（x、y）的集合，外加一個無窮遠點O（定義橢圓曲線上一個特殊的點，記為O，它為仿射平面無窮遠的點，稱為無窮遠點。在xOy平面上，可以看做平行于y軸的所有直線的集合的一種抽象）。

動態 | 中國銀行報告：區塊鏈在金融領域前景廣闊，數字貨幣是核心應用之一:中國銀行日前發布全球銀行業展望報告（2020年度）。報告指出，區塊鏈在金融領域應用前景廣闊，全球已有超過100家銀行進行了區塊鏈應用探索和布局，數字貨幣作為區塊鏈技術的核心應用之一，已獲得各國政府及中央銀行的廣泛關注。報告援引IBM和國際貨幣金融機構論壇（OMFIF）數據：目前全球73%的央行表示支持央行數字貨幣；38%的央行表示正在積極探索和試驗區塊鏈技術。“央行法定數字貨幣的推出會對貨幣發行、貨幣政策、支付清算、金融格局、互聯網金融發展乃至國際貨幣體系等方面產生極其深刻的影響。”[2020/1/2]

密碼學中普遍采用的是有限域上的橢圓曲線，它是指橢圓曲線方程定義式中，所有的系數都是在某一有限域GF（p）中的元素。它最簡單的公式為：

行情 | 數字貨幣早班車:截至8時05分，BTC全球均價 8796.07 美元，24小時漲幅 0.89 %；ETH全球均價 186.53 美元，24小時漲幅 1.00 %；EOS全球均價 3.48 美元，24小時漲幅 1.25 %。市值排名前百幣種中，24小時漲幅榜前五的是：HAV 24小時漲幅 18.45 %、KMD 24小時漲幅 15.73 %、MAN 24小時漲幅 10.74 %、NEO 24小時漲幅 9.03 %、VET 24小時漲幅 8.38 %。據統計，全球數字貨幣已超過 1477 種，TOP100總市值為 2,321.96億美元。[2019/11/13]

該橢圓曲線上只有有限個離散點，設為N，則N稱為橢圓曲線的階為N。N越大，安全性越高。基于此，橢圓曲線的圖示可以表示如下：

聲音 | 清華經管學院院長白重恩：數字金融資產天生是國際化的:據核財經消息，今日，由比特大陸捐贈的清華大學經濟管理學院數字金融資產研究中心正式成立。成立大會上，清華經管學院院長白重恩表示，數字金融資產天生是國際化的，但是目前在這方面的理論深度和學術指引都比較弱，實踐者創造了很多詞，給大眾創造了很多困擾。[2018/11/2]

當然，基于不同變量值，橢圓曲線還有其他的表示形式：

當我們仔細觀察這些曲線時，能發現一些有趣特性：（1）對稱性，即曲線上的任何一點都可以在x軸上反射，并保持曲線不變；（2）任何非垂直直線與曲線的交點至多有三個。

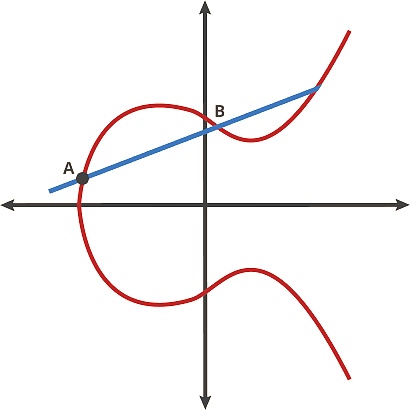
我們可以把這條曲線想象成一場桌球游戲。在曲線上取任意兩點并通過它們畫一條直線，它將與曲線相交于另一個位置。在這個桌球游戲中，你在A點拿一個球，把它射向B點，當它擊中曲線時，球要么直接向上反彈(如果它在x軸以下)，要么直接向下反彈(如果它在x軸以上)到曲線的另一邊。我們可以把球看做在兩個點間移動，曲線上的任意兩點碰撞可得到一個新的點。

A·B = C

或者可以用某一個點自身不斷碰撞出新的點。

A·A = B

A·C = D

……

在這個過程中，一個初始點經由n次運算會得到最后到達的點，當你只知道這兩個點的值，要找出n是很難的。

這就像一個人在房間里隨機玩一段時間桌球游戲，對他而言，按照上面描述的規則一遍又一遍地擊球是很容易的。但如果有人走進房間，球剛好結束到達一個點，即使他知道所有的游戲規則，以及球從哪個點開始，也不能確定球到達此處所被擊中的次數。容易正向計算，難以反向計算，這也是陷門函數的基礎。

1985年，Koblitz和Miller將橢圓曲線引入密碼學，提出了基于有限域GF（p）的橢圓曲線上的點集構成群，在這個群上定義離散對數難題并構造出基于其的一類公鑰密碼體制，即基于橢圓曲線的離散密碼體制，其安全性基于橢圓曲線上離散對數問題的難解性。

我們以基于橢圓曲線的ECDSA數字簽名實現方案為例，闡述其具體的實現過程。

密鑰生成算法

假設GF（p）為有限域，E是有限域GF（p）上的橢圓曲線。選擇E上一點G∈E，G的階為滿足安全要求的素數n，即nG=O（O為無窮遠點）。

選擇一個隨機數d，d∈[1，n-1]，計算Q，使得Q=dG。那么公鑰為（n，Q），私鑰為d。

簽名算法

假設待簽名的消息為m，經過如下計算過程，簽名者對消息m的數字簽名為（r，s）。

驗證算法

簽名接收者B對消息m簽名（r，s）的驗證過程如下：

判斷r和r1的關系，如果相等，則簽名有效；否則，簽名無效。

除了上述介紹ECDSA方案之外，基于橢圓的數字簽名方案還有很多，而類似DSA的其他方案例如Schnorr、EIGamal等方案也都被移植到橢圓曲線有限群上。

從上述介紹可知，數字簽名的安全性依賴于基于橢圓曲線的有限群上的離散對數難題。

與前章所述RSA數字簽名和基于有限域離散對數的數字簽名相比，基于橢圓曲線的數字簽名方案具有如下特點：在相同的安全強度條件下，簽名長度短，密鑰存儲空間小，適用于存儲空間有限，帶寬受限、要求高速實現的場合。

此外，橢圓曲線資源豐富，同一有限域上存在著大量不同的橢圓曲線，這也為安全性增加了額外的保障。

正是由于橢圓曲線具有豐富的群結構和多選擇性，并可以在保持和RSA、EIGamal體制同樣安全性的前提下大大縮短密鑰長度，因而有著更為廣闊的應用場景。

Tags：數字貨幣區塊鏈元宇宙數字金融加密貨幣和數字貨幣的區別是什么區塊鏈幣排名元宇宙幣種數字金融科技

UNI