零知識證明的寒武紀大爆炸_STA

這篇文章適用于具有一定密碼學背景的人。它調查了不斷擴展的證明系統密碼學以及對稱STARK在其中的作用。基于2019年11月在舊金山發表的演講。

1.簡介

35億年來，地球上的生命都是由單細胞生物組成的。然后，在地質學上的一眨眼之間，在所謂的寒武紀大爆發期間，幾乎所有我們今天認識的動物門類都出現了。

通過類比，我們目前正在經歷計算完整性(CI)加密證明領域的寒武紀大爆發，其中一個子集包括零知識證明。幾年前，每年大約有1-3個新系統，而現在這個速度已經加快了很多，如果不是每周，我們每個月都能看到同樣的數量。到目前為止，在2019年，我們已經了解了Libra,Sonic,SuperSonic,PLONK,SLONK,Halo,Marlin,Fractal,Spartan,SuccinctAurora等新結構，以及OpenZKP,Hodor和GenSTARK等實現。哦，當墨水在這篇文章上干燥時，RedShift和AirAssembly出現了。

如何理解所有這些了不起的創新?這篇文章的目的是找出所有用代碼實現的CI系統的共同點，并討論一些區別因素。

請注意，本文將有點技術性，因為它假定有一些密碼學背景!然而，對于感興趣的非密碼學家來說，這可能值得略讀一下，以了解該領域使用的術語。盡管如此，我們的描述將是簡短的，并且從數學的角度來看故意不精確。這篇文章的另一個主要目的是解釋為什么我們公司StarkWare將其所有的科學、工程和產品芯片放在CI-verse的一個特定子家族上，從此稱為對稱STARKs。

共同的祖先

計算完整性證明系統可以幫助解決困擾去中心化區塊鏈的兩個基本問題:隱私和可擴展性。零知識證明(ZKPs1)通過屏蔽計算的某些輸入而不損害完整性來提供隱私。簡潔可驗證的CI系統通過指數級壓縮驗證大量事務完整性所需的計算量來提供可伸縮性。

所有用代碼實現的CI系統都有兩個共同點:都使用所謂的算術化，并且所有加密都強制執行稱為“低程度遵從性”(LDC)2的概念。

LayerZero Labs 與 Polyhedra Network 合作推出基于零知識證明的輕客戶端:5月31日消息，LayerZero Labs 宣布與 Polyhedra Network 達成戰略合作，共同推出基于零知識證明技術的輕客戶端，使得 LayerZero 的開發者只需要更新一個參數配置就可以使用 Polyhedra Network 開發的零知識證明協議。[2023/6/1 11:51:12]

算術化是對證明算法所做的計算陳述的簡化。你可以從這樣一個概念性的陳述開始:

“我知道允許我進行加密Zcash交易的密鑰”

并將其轉化為包含一組有界多項式的代數語句，如:

“我知道四個多項式A(X)，B(X)，C(X)，D(X)，每一個都小于1000度，因此這個等式成立:A(X)*B2(X)-C(X)=(X1??-1)*D(X)”

低次遵從意味著使用密碼學來確保證明者實際上選擇了低次多項式3，并在驗證者請求的隨機選擇的點上評估這些多項式。在上面的例子中(我們將在這篇文章中繼續提到)，一個好的最不發達國家解決方案向我們保證，當證明者被問及x0時，它將回答a0,b0,c0,d0，這些值是輸入x0時a,b,c和d的正確值。棘手的部分是，證明者可能在看到查詢x0后選擇a,B,C和D，或者可能決定用任意的a0,B0,C0,D0來安撫驗證者，并且不對應于預先選擇的低次多項式的任何評估。所以，所有的加密技術都是為了防止這種攻擊媒介。(要求證明者發送完整的A、B、C和D的平凡解決方案既不能提供可伸縮性，也不能提供隱私。)

考慮到這一點，CI-verse可以根據(i)用于強制LDC的加密原語，(ii)使用這些原語構建的特定LDC解決方案以及(iii)這些選擇允許的算法類型來繪制。

2.比較維度

i.密碼學假設

從30000英尺的角度來看，不同CI系統之間最大的理論區別因素是它們的安全性是需要對稱基元還是不對稱基元(參見圖1)。典型的對稱基元是SHA2、Keccak(SHA3)或Blake，我們假設它們是抗碰撞哈希(CRH)函數、偽隨機函數，其行為就像隨機的oracle。非對稱假設包括求解以素數、RSA模數或橢圓曲線群為模的離散對數問題的難度，計算RSA環的乘法群的大小的難度，以及此類問題的更奇特的變體，如“指數知識”假設，“自適應根”假設等。

零知識證明技術公司Proven完成1580萬美元融資:金色財經報道，Proven是一家提供零知識證明技術以使加密貨幣公司能夠證明償付能力的公司，完成1580萬美元種子輪融資，Framework Ventures領投，Balaji Srinivasan、Roger Chen和Ada Yeo等參投。[2023/3/9 12:52:34]

圖1:密碼學假設家譜

CI系統之間的這種對稱/不對稱劃分有許多后果，其中包括:

A.計算效率

今天在代碼中實現的非對稱原語的安全性需要在大型代數域上進行算術運算并解決LDC問題:大型素域和它們上面的大型橢圓曲線，其中每個域/組元素都是數百位長，或者整數環，其中每個元素都是數千位長。相比之下，僅依賴對稱假設的構造在任何代數域(環或有限域)上進行算術運算并執行LDC，這些代數域包含光滑的5子群，包括非常小的二進制域和2-光滑素域(64位或更少)，其中算術運算很快。

結論:對稱CI系統可以在任何領域進行算術運算，從而提高效率。

B.后量子安全

如果有足夠大的量子計算機(以量子位為單位)出現，那么目前在ci領域中使用的所有不對稱原語都將被有效地打破。另一方面，對稱原語似乎是后量子安全的(可能每比特安全性具有更大的種子和狀態)。

結論:只有對稱系統才是后量子安全的。

圖2:加密假設及其支持的經濟價值

C.能否經得住時間的考驗

林迪效應理論認為，“一些不易腐爛的東西，比如技術或想法，未來的預期壽命與它們當前的年齡成正比。”或者用簡單的英語來說，舊的東西比新的東西存活的時間更長。在密碼學領域，這可以被翻譯為說依賴于舊的、經過戰斗測試的原語的系統比那些經過較少考驗的新假設更安全，更經得起未來的考驗(見圖2)。從這個角度來看，不對稱假設的新變體，如未知順序的組，一般的群體模型和指數假設的知識是年輕的，并且比舊的假設(如用于數字簽名，基于身份的加密和SSH初始化的更標準的DLP和RSA假設)更輕的經濟車。這些假設不如對稱假設(如抗碰撞哈希的存在)具有前瞻性，因為后者的假設(甚至是特定的哈希函數)是用于保護計算機、網絡、互聯網和電子商務的基礎。

以太坊生態零知識協議Semaphore發布V2版本:7月7日消息，以太坊生態針對開發者的零知識協議 Semaphore 推出 V2 版本，更新內容包括不再需要擁有 EdDSA 私鑰，從而實現更簡單的電路（circuit）和更高效的零知識證明生成；用于身份承諾和 Merkle 樹的哈希函數從 MiMC 遷移到 Poseidon，將證明時間減半并提高了 Gas 效率；合約模塊化、三個新的 JavaScript 庫等。

Semaphore 最早由以太坊社區成員 Kobi Gurkan、Koh Wei Jie 和 Barry Whitehat 提出，在 2019 年發布 V1 版，可以讓以太坊用戶可以證明他們的群組成員身份，并在不透露原始身份的情況下發送諸如投票或支持的信號。Semaphore 不是面向用戶的應用程序，旨在為以太坊開發人員提供強大而簡單的工具，以使用私有憑據構建 DApp。[2022/7/7 1:57:35]

此外，這些假設之間有嚴格的數學層次關系。CRH假設在這個層次結構中占主導地位，因為如果這個假設被打破(意味著沒有找到安全的加密哈希函數)，那么RSA和DLP假設也會被打破，因為這些假設意味著存在一個好的CRH!同樣，DLP假設支配著指數知識(KoE)假設，因為如果前者(DLP)假設不成立，那么后者(KoE)也不成立。同樣，RSA假設優于未知順序組(GoUO)假設，因為如果RSA被破壞，那么GoUO也會被破壞。

結論:新的不對稱假設是金融基礎設施風險更高的基礎。

D.參數長度

以上所有觀點都傾向于對稱CI結構而非對稱CI結構。但在一個領域，不對稱結構表現得更好。與之相關的溝通復雜性(或參數長度)要小1-3個數量級(盡管有尼爾森定律6)。眾所周知，Groth16SNARK在估計的128位安全級別上小于200字節，而目前存在的所有對稱結構都需要數十千字節才能達到相同的安全級別。應該注意的是，并非所有的非對稱結構都像200字節那樣簡潔。最近的結構改進了Groth16，通過(i)消除了對可信設置(透明度)的需要和/或(ii)處理一般電路(Groth16每個電路需要一個可信設置)。但是這些較新的結構具有更長的參數，其大小在半千字節(PLONK的情況就是如此)到兩位數的千字節之間，接近對稱結構的參數長度。

動態 | 波場TRON網絡即將進行零知識證明匿名交易公測:據官方最新消息，波場TRON網絡即將進行零知識證明匿名交易公測，現在誠邀社區參與MPC過程，參與者越多，匿名交易越安全。通過參與MPC，用戶可以將貢獻永久的保存在TRON網絡中。參考見原文鏈接。[2019/12/19]

結論:非對稱電路專用系統(Groth16)最短，比所有非對稱通用系統和所有對稱系統都短。

重申上述要點:

對稱CI系統可以對任何領域進行算術運算，從而提高效率

只有對稱系統才是后量子安全的

新的不對稱假設為金融基礎設施奠定了一個風險更高的基礎

非對稱電路專用系統(Groth16)最短，比所有非對稱通用系統和所有對稱系統都短

ii.低程度合規計劃

實現低程度遵從性有兩種主要方法:(i)隱藏查詢和(ii)承諾方案(參見圖3)。讓我們來看看它們之間的區別。

圖3:隱藏查詢和承諾方案

隱藏查詢

這種方法(在這里形式化)是Zcash風格的snark(如Pinocchio,libSNARK,Groth16)以及基于它們的系統(如Zcash的Sapling，以太坊的Zokrates等)所使用的方法。為了讓證明者正確回答，我們使用同態加密來隱藏或加密x0，并提供足夠的信息，以便證明者可以計算x0上的A,B,C和D。實際上，給證明者的是x0的冪的加密序列(即x01，x02，…x01??)，因此證明者可以計算任何1000次多項式，但只能計算最多1000次的多項式。粗略地說，這個系統是安全的，因為證明者不知道x0是什么，這個x0是隨機(預先)選擇的，所以如果證明者試圖作弊，那么他們很有可能會被暴露。這里需要一個可信的預處理設置階段來對x0進行采樣并加密上述冪次序列(以及其他信息)，從而產生一個至少與被證明的計算電路一樣大的證明密鑰(也有一個短得多的驗證密鑰)。一旦設置完成，密鑰被釋放，每個證明都是一個單一的、簡潔的、非交互式的知識論證(簡稱SNARK)。請注意，這個系統確實需要某種形式的交互，以預處理階段的形式，這是不可避免的理論原因。還要注意的是，該系統并不透明，這意味著用于采樣和加密x0的熵不能僅僅是公共隨機硬幣，因為任何知道x0的人都可以破壞該系統并證明錯誤。因此，在不泄露x0的情況下生成x0及其功率的加密是一個構成潛在單點故障的安全問題。

動態 | 以色列理工學院教授違反知識產權規定建立零知識證明技術公司:據Bitcoin.com報道，以色列理工學院教授Eli Ben-Sasson因違反了該學校知識產權規定而被起訴。據報道，Ben-Sasson利用在為該機構工作時開發的知識產權建立了一家零知識證明技術公司。Ben-Sasson是區塊鏈技術初創公司Starkware的聯合創始人兼首席科學家，以色列理工學院在法庭提出要求Ben-Sasson轉讓其在該公司的50%股份。[2019/4/23]

承諾方案

這種方法要求證明者通過向驗證者發送一些加密的承諾消息來提交一組低次多項式(A、B、C和D，在上面的例子中)。有了這個承諾，驗證者現在采樣并詢問證明者隨機選擇的x0，現在證明者回復a0,b0,c0和d0以及額外的加密信息，這些信息使驗證者相信證明者透露的四個值符合早先發送給驗證者的承諾。這些方案是自然交互的，其中許多是透明的(驗證者生成的所有消息都是公共隨機硬幣)。透明度允許人們通過Fiat-Shamir啟發式(將偽隨機函數(如SHA2/3)視為提供“公共”隨機性的隨機oracle)將協議壓縮為非交互式協議，或者使用其他公共隨機性來源，如塊頭。最流行的透明承諾方案是通過Merkle樹，這種方法似乎是后量子安全的，但會導致許多對稱系統中出現的大參數長度(由于需要顯示所有身份驗證路徑并伴隨每個證明者答案)。這是大多數STARK使用的方法，如libSTARK和簡潔的Aurora，以及簡潔的證明系統，如ZKBoo,Ligero,Aurora和Fractal(即使這些系統不滿足STARK的正式可擴展性定義)。特別是，我們在StarkWare上構建的STARKs(就像我們即將部署的StarkDEXalpha和StarkExchange)屬于這一類。人們可以使用不對稱原語來構建承諾方案，例如，基于橢圓曲線群上離散對數問題的硬度的方案(這是BulletProofs和Halo采用的方法)，以及未知階假設的組(如DARK和SuperSonic所做的)。使用不對稱承諾方案有前面提到的優點和缺點:較短的證明但較長的計算時間、量子敏感性、較新的(和較少研究的)假設，以及在某些情況下，透明度的喪失。

iii.算術化

加密假設和LDC方法的選擇也會以三種明顯的方式影響算術可能性的范圍(參見圖4):

圖4:算術化效果

A.NP(電路)vs.NEXP(程序)

大多數實現的CI系統將計算問題簡化為算術電路，然后將其轉換為一組約束(通常是R1CS約束，下面將討論)。這種方法允許特定電路的優化，但要求驗證者或受其信任的某些實體執行與被驗證的計算(電路)一樣大的計算。對于像Zcash的樹苗電路這樣的多用途電路，這種算法就足夠了。但是，像libSTARK、簡潔的Aurora和StarkWare正在構建的系統這樣的可擴展和透明(不受信任的設置)的系統，必須使用簡潔的計算表示，類似于一般的計算機程序，其描述比正在驗證的計算要小得多。實現這一目標的兩種現有方法是:(i)libSTARK、genSTARK和StarkWare系統使用的代數中間表示(AIRs)，以及(ii)簡潔R1CS的簡潔aurora，最好被描述為通用計算機程序的算術運算(與電路相反)。這些簡潔的表示足以捕獲非確定性指數時間(NEXP)的復雜性類，它比電路描述的非確定性多項式時間(NP)類更具指數性和強大。

B.字母的大小和類型

如上所述，所使用的密碼學假設也在很大程度上決定了哪些代數域可以作為我們進行算術運算的字母表。例如，如果我們使用雙線性配對，那么我們將用于算術化的字母表是橢圓曲線點的一個循環群，這個群必須是大素數，這意味著我們需要在這個域上進行算術化。再舉一個例子，超音速系統(在它的一個版本中)使用RSA整數，在這種情況下，字母表將是一個大的素數字段。相比之下，當使用Merkle樹時，字母表的大小可以是任意的，允許在任何有限的域上進行算術運算。這包括上面的例子，也包括任意素數域，小素數域的擴展，如二進制域。字段類型很重要，因為較小的字段會導致更快的證明和驗證時間。

C.R1CS與一般多項式約束

zcash風格的snark利用橢圓曲線上的雙線性對來對計算約束進行算法化。這種雙線性對的特殊使用?將算法限制在二次秩-1約束系統(R1CS)的門上。R1CS的簡單性和普遍性使得許多其他系統在電路中使用這種形式的算法，即使可以使用更一般形式的約束，如任意秩二次型，或更高程度的約束。

3.STARKvs.SNARK

這是一個很好的機會來澄清stark和SNARKs之間的區別。這兩個術語都有具體的數學定義，某些結構可以實例化為stark或snark，或兩者兼而有之。不同的術語強調證明系統的不同性質。讓我們更詳細地檢查一下(參見圖5)。

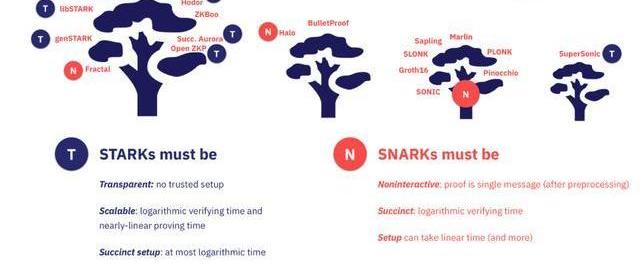
圖5:STARKvs.SNARK

STARK

這里的S代表可擴展性，這意味著隨著批大小n的增加，在n中準線性證明時間尺度，同時在n中多對數?驗證時間尺度。STARK中的T代表透明度，這意味著所有驗證者消息都是公共隨機幣(沒有可信設置)。根據這個定義，如果有任何預處理設置，那么它必須是簡潔的(多對數的)，并且必須僅包含對公共隨機硬幣的采樣。

SNARK

這里的S代表簡潔，這意味著驗證時間尺度在n上是多對數的(不要求準線性證明時間)，n意味著非交互，這意味著在預處理階段(可能是不透明的)之后，證明系統不能允許任何進一步的交互。請注意，根據這個定義，允許非簡潔的可信設置階段，一般來說，系統不必是透明的，但它必須是非交互式的(在完成預處理階段之后，這是不可避免的)。

看看CI-verse(見圖5)，人們注意到它的一些成員是STARKs，其他成員是SNARKs，有些是兩者都是，而另一些則兩者都不是(例如，如果驗證時間尺度比n的多對數更差)。如果你對隱私(ZKP)應用感興趣，那么ZK-SNARKs和ZK-STARKs甚至既沒有STARK的可擴展性也沒有SNARK的簡便性(較弱)的系統都可以很好地服務;門羅幣使用的防彈技術就是一個值得注意的例子，其驗證時間與電路尺寸呈線性關系。當談到代碼成熟度時，snark有一個優勢，因為有相當多好的開源庫可供構建。但是，如果您對可伸縮性應用程序感興趣(您需要為不斷增長的批處理大小構建)，那么我們建議使用對稱stark，因為在編寫時，它們具有最快的證明時間，并且保證驗證過程(或設置系統)的任何部分都不需要超過多對數的處理時間。如果你想構建具有最小信任假設的系統，那么，再一次，你想使用對稱的STARK，因為需要的唯一成分是一些CRH和公共隨機性的來源。

4.總結

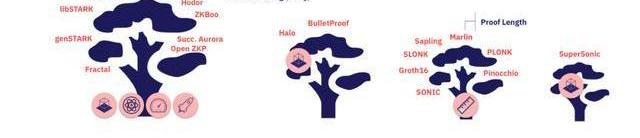
圖6:總結

我們有幸經歷了計算完整性證明系統宇宙的寒武紀大爆發，所有的賭注都是系統和創新的擴散將以越來越快的速度繼續下去。此外，隨著明天出現新的見解和結構，這種描述擴展和變化的CI-verse的嘗試可能會過時。話雖如此，調查今天的ci空間，我們看到的最大的分水嶺是(i)需要非對稱加密假設的系統-這導致更短的證明，但證明成本更高，有更新的假設，這些假設是量子敏感的，其中許多是不透明的;(ii)系統只依賴于對稱假設，使它們在計算上高效，透明，似乎是后量子安全的，而且是最未來的證明(根據林迪效應度量)。

關于使用哪種論證體系的爭論遠未結束。但在StarkWare，我們說:對于簡短的參數，使用Groth16/PLONKSNARKs。其他的都是對稱的STARKs。

伊萊·本·薩森，StarkWare公司

特別感謝JustinDrake對早期草稿的評論。

Billions項目組

Tags：ARKSTARSTAARK幣是什么幣STAR幣STAR價格STA幣STA價格

Ethereum