你可能不知道隱藏在楊輝三角形中的 10 個秘密！_ONS

楊輝三角形，又稱帕斯卡三角形、賈憲三角形、海亞姆三角形，它的排列形如三角形。因為首現于南宋楊輝的《詳解九章算法》得名，而書中楊輝說明是引自賈憲的《釋鎖算書》，故又名賈憲三角形。古代波斯數學家歐瑪爾·海亞姆也描述過這個三角形。在歐洲，因為法國數學家布萊茲帕斯卡在1653年的《論算術三角》中首次完整論述了這個三角形，故也被稱作帕斯卡三角(Pascal'striangle)。

楊輝三角的前10行寫出來如下：

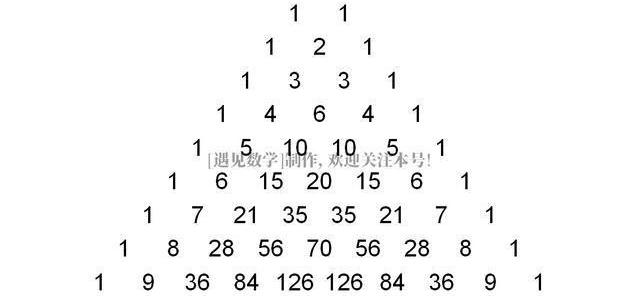
楊輝三角的構建

Treasure DAO推出成就勛章系統:5月24日消息，去中心化游戲生態系統Treasure DAO 為其生態 NFT 平臺推出成就勛章系統。用戶可根據在 Treasure 上的行為記錄和購買記錄領取不同級別的靈魂綁定勛章，從而提升用戶的互操作體驗。[2023/5/24 15:23:06]

在最上面一行的中央寫下數字1第二行，寫下兩個1，和上一行形成三角形隨后的每一行，開頭和最后的數字都是1，其他的每個數都是它左上方和右上方的數之和，就是說除每行最左側與最右側的數字以外，每個數字等于它的左上方與右上方兩個數字之和。

左對齊后的楊輝三角前兩列倒沒什么特別的地方，第一列均為1，第二列則為自然數。而第三列就是三角形數(Triangularnumber)。你可以想到，三角數就是能夠組成大大小小等邊三角形的點的數目，如下圖所示。

特斯拉在第四季度沒有買賣任何比特幣:金色財經報道，電動汽車制造商特斯拉 (TSLA) 在其最新的收益報告中稱，其在第四季度連續第二個季度沒有購買或出售任何比特幣。其數字資產的價值為 1.84 億美元，低于第三季度末的 2.18 億美元，原因是比特幣價格下跌導致的減值費用。第三季度末，比特幣價格略低于 20,000 美元，而第四季度末約為 16,500 美元。

特斯拉在第三季度也沒有改變其比特幣持有量，但在第二季度，該公司出人意料地出售了價值 9.36 億美元的比特幣，約占其總持有量的 75%，以籌集現金。[2023/1/26 11:30:08]

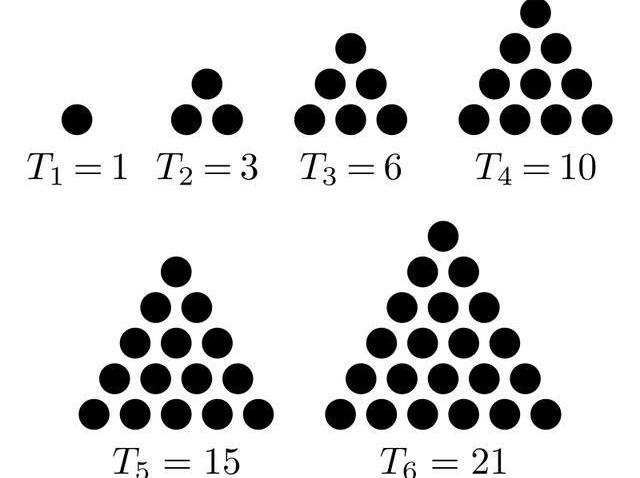
三角形數(圖自維基)類似地，第四列是四面體數(Tetrahedralnumber)，也叫三角錐體數。顧名思義，它們代表由三角形構成的四面體所需要的點的數目，四面體數每層為三角形數。

區塊鏈制藥數據交換系統開發公司ServBlock獲歐盟資金支持:金色財經報道，愛爾蘭區塊鏈制藥數據交換系統開發公司ServBlock宣布已獲得歐盟資金支持，旨在構建可信數據交換系統，ServBlock 使用區塊鏈或分布式賬本技術來確保制藥和醫療保健供應鏈的可追溯性、隱私性和透明度，為制藥供應鏈中的可信數據傳輸提供測試用例，該公司已收到歐盟 i4Trust 計劃與愛爾蘭制造研究組織 IMR聯合提供的資金（具體金額暫未披露），以支持創新研發項目。（irishtimes）[2022/12/20 21:56:12]

圖自維基秘密Billions項目組3：11的冪

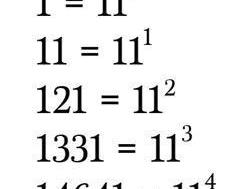
Across Protocol：治理代幣ACX的相關代碼工作已完成:11月19日消息，跨鏈橋Across Protocol發推稱，治理代幣ACX的相關代碼工作已完成。

此前消息，Across Protocol已宣布將于11月28日發行ACX。[2022/11/19 7:47:58]

楊輝三角還揭示了11為底的冪的值。你要做的就是將每一行的數字擠壓到一起。前5行足夠簡單，但出現兩位數的時候該怎么辦呢？

事實證明，你要做的就是將十位數加到它左側數字上，比如下圖所示的是第六行中出現了上面的情況，如何進行移動以獲得11的值

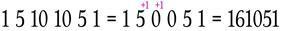
如果出現了三位數同樣進位處理即可。

數據：近24小時全網爆倉2.48億美元，以太坊爆倉1.15億美元:金色財經報道，據Coinglass數據，近24小時全網爆倉2.48億美元，其中比特幣爆倉4320.01萬美元，以太坊爆倉1.15億美元。[2022/11/5 12:19:34]

秘密Billions項目組5:斐波那契數列

為了揭示隱藏的斐波那契數列，將左對齊的楊輝三角對角線相加。比如下圖楊輝三角中發現的斐波那契數列前九個數：1，1，2，3，5，8，13，21，34…

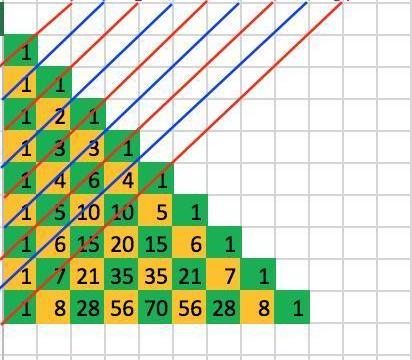
按線條所示相加結果即為斐波那契數列秘密Billions項目組7:組合數學

或許楊輝三角中發現的最有趣的關系就是我們如何利用它找到組合數。

楊輝三角的前六行寫成組合數的表達形式回憶一下從n個不同元素中選k個元素的組合公式。我們發現，對于楊輝三角中的每一行數字，從零開始計數，n是行數，k是在這一行中的位置。

所以，如果你想計算4選2，看第5行，第3個數，你會發現，答案是6.

秘密Billions項目組9:二項式定理

(x+y)的冪運算是很酷，但我們多久才會需要解這樣的題呢？很有可能，不太經常需要。如果我們能夠從上一個章節的結論中總結出一個更有用的形式，會不會更方便？好吧，其實這就是二項式定理：

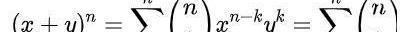
這個公式也稱二項式公式或二項恒等式。

更具體內容請見文章《利用楊輝三角形來解釋二項式定理》

秘密#10:與概率之間的聯系—二項式分布

二項式分布描述了具有兩種可能結果的實驗的概率分布。事實上，楊輝三角的每一行也能揭示了這樣的清晰，以最經典就是扔一枚硬幣為例吧。

如果考慮拋3次硬幣，就會有8種可能發生的事件：

但其實可以分為4類情況：

3次反面——只有1次發生2次正面和1次反面——有3次發生2次反面和1次正面——有3次發生3次正面——只有1次發生這注意1,3,3,1正是楊輝三角的第4行。同樣如果拋5次硬幣，出現3正2反的事情會出現10次，這也是出現在了楊輝三角第6行。

如果設拋硬幣得到正面概率為p，反面概率為1–p。想知道扔到正面的可能性，我們可以使用二項式分布的概率質量函數找到概率的分布，其中n是試驗次數，k是成功次數。

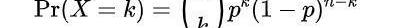
二項式分布的概率質量函數嗨，這看起很熟悉啊！這幾乎和我們前面提到的二項式定理是一樣的公式，只是沒有求和公式，同時x和y被p和1-p代替了。

假設成功的概率是0.5(p=0.5)，我們計算扔到正面0次、1次、2次、3次的概率。

在公式中代入n=3、k=0,1,2,3，得到下面計算結果，請注意楊輝三角里的組合數：1,3,3,1：

扔到正面0次、3次的可能性都是12.5%，而扔到正面1次、2次的可能性都是37.5%，這與上面分析結果是一致的。

這便是看似簡單的楊輝三角里的10個秘密，是不是很精彩啊！但這并不是終點，還有另外更有趣的性質隱藏其中，或許未來我們繼續前行，一道再探索吧。

本文作者：姚高華、李千蔚

Tags：IONLIOONSLIONIONChainNeblioCONST價格treelion

MANA